| Tandem Project Leader | Carsten Rockstuhl |
| NHR@KIT Project Leader | Martin Frank |
| Project Coordinator | Ivan Kondov |
| Team | SDL Material Science |
| Researchers | Lina Kuhn & Maria Paszkiewicz |
| Open source software | - |
Introduction
This project uses artificial neural networks as surrogate models in an inverse design problem of finding nano-structured materials with optical properties on demand. Achieving this goal requires to generate large amounts of data from 3D simulations of Maxwell's equations, which makes this a data-intensive computing problem. Tailored algorithms and code will be developed that address both the learning and the efficient inversion. The project complements research in the SDL Materials Science on AI methods, large data sets generated by simulations, and workflows. The project will not only have an impact on the applications but will also lead to a better understanding of data generation by simulations for the training of neural networks and how such a strategy can be implemented.
The ability to design photonic materials with predefined properties to mold the flow of light is an intellectual challenge and of utmost importance in many impact areas such as sensing, imaging, or emerging quantum technologies. Using artificial neural networks will accelerate the design process to a considerable extent. Moreover, accommodating constraints from possible fabrication technologies, as we aim for in this project, guarantees the realization of designed structures with existing tools. With the establishment of such technology, we directly impact a significant amount of cooperation.
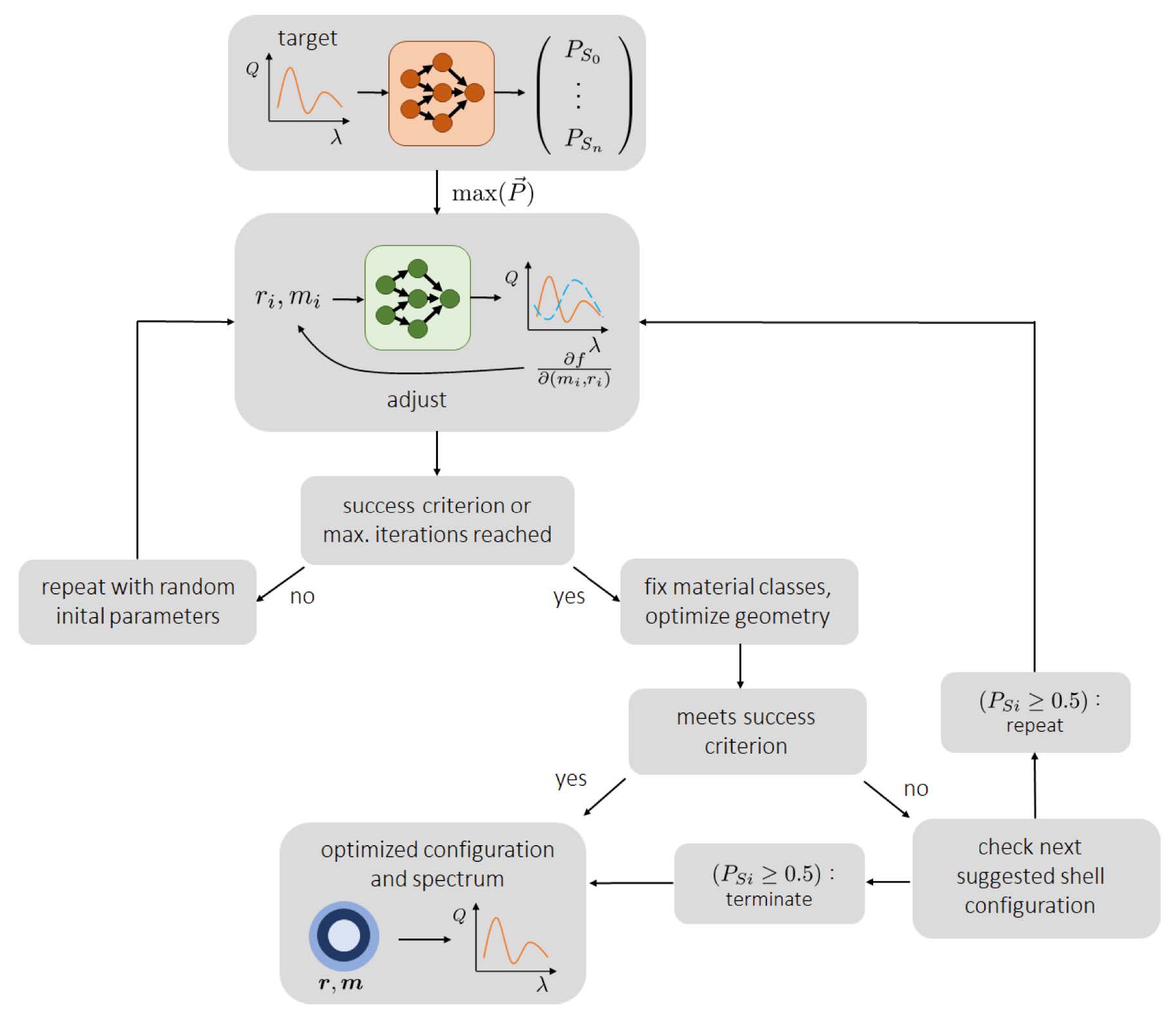
Figure: A neural network to inversely design spherical core-multishell scattereres. A classifier (orange) suggests the number of shells most likely necessary to provide a desired spectrum. A DNN solves highly efficient the forward problem (green) which allows to use gradient-based methods to optimize the degrees of freedom.
Project description
Nano-structured materials provide unprecedented degrees of freedom to control light. This ability is of paramount importance when considering devices out of intellectual curiosity and perceiving applications with impact at the societal level. One example for the former, out of our research portfolio, are meta-surfaces made from periodically arranged scatterers that serve as light sails suggested for the Breakthrough Starshot Initiative. The initiative's purpose is to develop gram satellites, accelerated by earth-based laser arrays to a substantial fraction of the speed of light, to explore the space beyond our solar system, i.e., Proxima Centauri B. One example for the latter would be photonic cavities out of meta-surfaces that enhance the light while preserving its helicity, i.e., the circular polarization. Such cavities improve our ability to sense the circular dichroism from molecules. Cavities with an enhancement factor of 100 reduce the measurement time from ten hours to only six minutes, which is tremendously important for the (nearly) real-time characterization of drugs in production lines.
These and other devices can be designed using a parametric representation of the optical properties of the scatterer from which meta-surfaces are made. These parameters constitute the base for an algebraic description of the light-matter-interaction. In this description, incident and scattered fields are expanded into basis functions, and matrix multiplication connects both. The connecting matrix is called the T-matrix, and its size depends on the truncation order. The T-matrix is a frequency-dependent quantity, and it contains all the information on how an object scatters an incident field.
For a given object, the T-matrix can be computed from the geometry and the material composition of an object by solving the full-wave 3D Maxwell equations. One simulation takes between a millisecond for a sphere up to a few tens of minutes for complicated structures on a single thread. The actual computation might take many hours if the T-matrix needs to be spectrally resolved. This constitutes the forward problem and is at the heart of the data generation. However, the actual challenge is to solve the inverse problem. This requires identifying a physically existing object from some given materials that offers a predefined T-matrix. This inverse problem is much harder to solve but also much more rewarding.
This high-risk-high-gain project aims to use artificial neural networks as a surrogate model for the map that assigns a T-matrix to a specific object. This allows to speed up the forward problem, but, most importantly, it enables a fast search of the parameter space to solve the inverse design problem.
Once we know the most optimal T-matrix for a specific application, our second challenge concerns designing an object that offers the desired T-matrix. The design, ideally, should be constrained by existing materials and geometries accessible by available fabrication technologies to realize these scatterers. As an example of such fabrication technology, we concentrate on materials fabricated with either 3D laser lithography or with DNA origami of clusters of metallic nanoparticles.
The HPC challenge lies in the data generation, which is done by simulations. A further challenge lies in learning with additional restrictions, such as restrictions on the objects to be feasible for fabrication with an existing technology or stability properties of the identified objects. This will require adapting both the learning (especially the simulations, which will be equipped with uncertainties) and the inversion.
The project concentrates on the development of the tools and the demonstration of their applicability. An HPC environment is necessary due to the sheer complexity of the addressed problems. This concerns the computational needs to link a given structure to its optical properties (Maxwell solver), the amount of data required to train neural networks, and the actual training process. But the overall speed-up of the recurring task to design scatterers with properties on demand is worth the effort.